statmechcrack.isometric

A module for the crack model in the isometric ensemble.

This module consist of the class CrackIsometric which contains methods for computing quantities in the isometric (constant displacement) thermodynamic ensemble.

class CrackIsometric(**kwargs)[source]

Bases: CrackMonteCarlo

The crack model class for the isometric ensemble.

Q_0_isometric(v, lambda_)[source]

The nondimensional isometric partition function as a function of the nondimensional end separation for the reference system,

\[Q_0(v,\boldsymbol{\lambda}) = Q_b(v,\lambda_1,\lambda_2) e^{-\beta U_{01}(\boldsymbol{\lambda})}.\]
Parameters:

  • v (array_like) – The nondimensional end separation.

  • lambda (array_like) – The intact bond stretches.

Returns:

The nondimensional isometric partition function.

Return type:

numpy.ndarray

Example

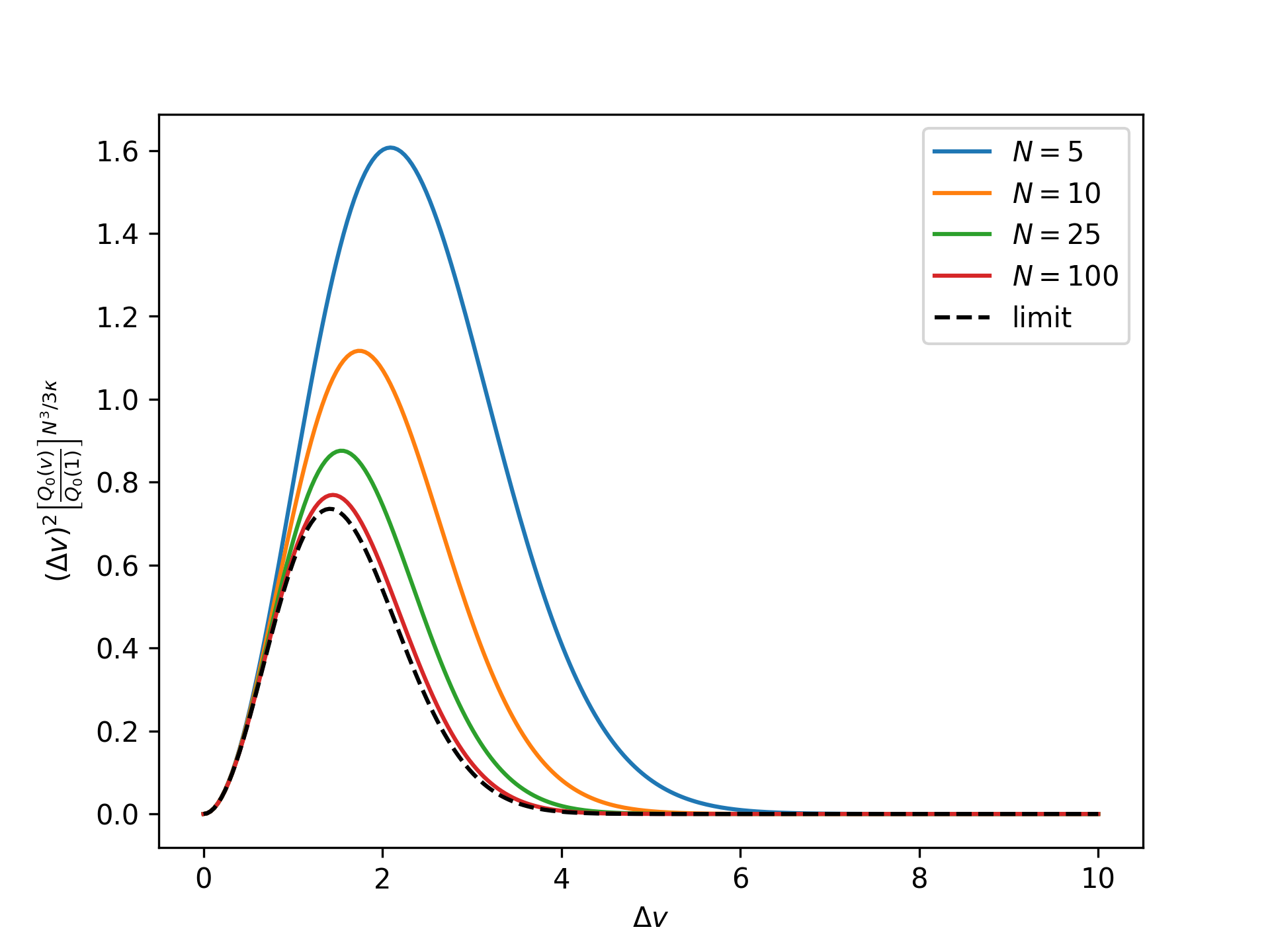
Plot the rescaled nondimensional equilibrium radial distribution as a function of the nondimensional end separation for the reference system in the isometric ensemble for an increasing number of broken bonds \(N\) and compare to the thermodynamic limit:

>>> import numpy as np
>>> import matplotlib.pyplot as plt
>>> from statmechcrack import CrackIsometric
>>> v = np.linspace(1, 11, 250)
>>> _ = plt.figure()
>>> for N in [5, 10, 25, 100]:
...     model = CrackIsometric(N=N)
...     r_Q_0 = (model.Q_0_isometric(v, [1, 1])
...         / model.Q_0_isometric(1, [1, 1])
...     )**(model.N**3/3/model.kappa)
...     _ = plt.plot(v - 1, (v - 1)**2*r_Q_0,
...                  label='$N=$'+str(N))
>>> _ = plt.plot(v - 1, (v - 1)**2*np.exp(-(v - 1)**2/2),
...              'k--', label='limit')
>>> _ = plt.xlabel(r'$\Delta v$')
>>> _ = plt.ylabel(r'$(\Delta v)^2$' +
...     r'$\left[\frac{Q_0(v)}{Q_0(1)}\right]^{N^3/3\kappa}$')
>>> _ = plt.legend()
>>> plt.show()
_images/statmechcrack-isometric-1.png
Q_b_isometric(v, lambda_)[source]

The nondimensional isometric partition function as a function of the nondimensional end separation for the isolated bending system,

\[Q_b(v,\lambda_1,\lambda_2) = \sqrt{\frac{(2\pi)^N}{\det\mathbf{H}}} \,e^{\frac{1}{2}\mathbf{g}^T\cdot\mathbf{H}^{-1}\cdot\mathbf{g}-f},\]

where \(\mathbf{H}\), the nondimensional Hessian of the potential energy for the isolated bending system, and \(\mathbf{g}\) and \(f\) are

\[\mathbf{g}(v,\lambda_1,\lambda_2) = \kappa\left( 2v, -v, 0, \ldots, 0, -\lambda_1, 4\lambda_1 - \lambda_2 \right)^T,\]
\[f(v,\lambda_1,\lambda_2) = \frac{\kappa}{2}\left[v^2 + \lambda_1^2 + \left(2\lambda_1 - \lambda_2\right)^2\right] .\]
Parameters:

  • v (array_like) – The nondimensional end separation.

  • lambda (array_like) – The intact bond stretches.

Returns:

The nondimensional isometric partition function.

Return type:

numpy.ndarray

Q_isometric(v, transition_state=False)[source]

The nondimensional isometric partition function as a function of the nondimensional end separation,

\[Q(v) = \int d\lambda \ Q_0(v,\boldsymbol{\lambda}) e^{-\beta U_1(\boldsymbol{\lambda})},\]

approximated using the asymptotic relation

\[Q(v) \sim Q_0(v, \hat{\boldsymbol{\lambda}}) \prod_{j=1}^M \sqrt{\frac{2\pi}{\beta u''(\hat{\lambda}_j)}} \, e^{-\beta u(\hat{\lambda}_j)},\]

which is valid for \(\varepsilon\gg 1\), where \(\hat{\boldsymbol{\lambda}}\) is from minimizing \(\beta U\).

Parameters:

  • v (array_like) – The nondimensional end separation.

  • approach (str, optional, default='asymptotic') – The calculation approach.

  • transition_state (bool, optional, default=False) – Whether or not to calculate in the transition state.

Returns:

The nondimensional isometric partition function.

Return type:

numpy.ndarray

Example

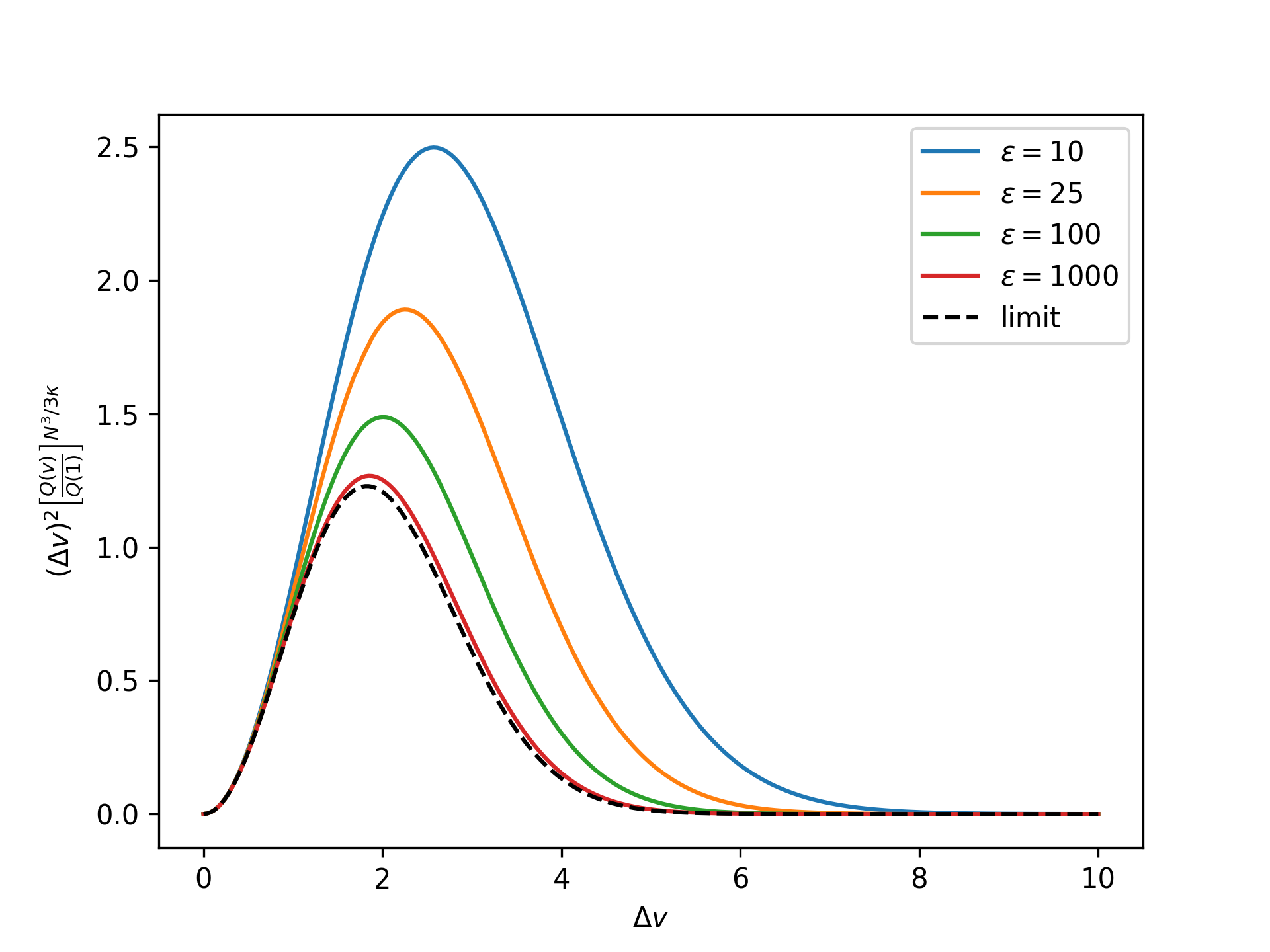
Plot the rescaled nondimensional equilibrium radial distribution as a function of the nondimensional end separation in the isometric ensemble for an increasing nondimensional bond energy and compare to the limit given by the reference system:

>>> import numpy as np
>>> import matplotlib.pyplot as plt
>>> from statmechcrack import CrackIsometric
>>> v = np.linspace(1, 11, 250)
>>> _ = plt.figure()
>>> for varepsilon in [10, 25, 100, 1000]:
...     model = CrackIsometric(varepsilon=varepsilon)
...     r_Q = (model.Q_isometric(v)/model.Q_isometric(1)
...     )**(model.N**3/3/model.kappa)
...     _ = plt.plot(v - 1, (v - 1)**2*r_Q,
...                  label=r'$\varepsilon=$'+str(varepsilon))
>>> r_Q_0 = (model.Q_0_isometric(v, [1, 1])
...     / model.Q_0_isometric(1, [1, 1])
... )**(model.N**3/3/model.kappa)
>>> _ = plt.plot(v - 1, (v - 1)**2*r_Q_0,
...              'k--', label='limit')
>>> _ = plt.xlabel(r'$\Delta v$')
>>> _ = plt.ylabel(r'$(\Delta v)^2$' +
...     r'$\left[\frac{Q(v)}{Q(1)}\right]^{N^3/3\kappa}$')
>>> _ = plt.legend()
>>> plt.show()
_images/statmechcrack-isometric-2.png
beta_A_0_abs_isometric(v, lambda_)[source]

The absolute nondimensional Helmholtz free energy as a function of the nondimensional end separation for the reference system,

\[\beta A_0(v,\boldsymbol{\lambda}) = -\ln Q_0(v,\boldsymbol{\lambda}) = \beta A_b(v,\lambda_1,\lambda_2) + \beta U_{01}(\boldsymbol{\lambda}).\]
Parameters:

  • v (array_like) – The nondimensional end separation.

  • lambda (array_like) – The intact bond stretches.

Returns:

The absolute nondimensional Helmholtz free energy.

Return type:

numpy.ndarray

beta_A_0_isometric(v, lambda_)[source]

The relative nondimensional Helmholtz free energy as a function of the nondimensional end separation for the reference system,

\[\beta\Delta A_0(v,\boldsymbol{\lambda}) = \beta A_0(v,\boldsymbol{\lambda}) - \beta A_0(v_0,\boldsymbol{\lambda}).\]
Parameters:

  • v (array_like) – The nondimensional end separation.

  • lambda (array_like) – The intact bond stretches.

Returns:

The relative nondimensional Helmholtz free energy.

Return type:

numpy.ndarray

Example

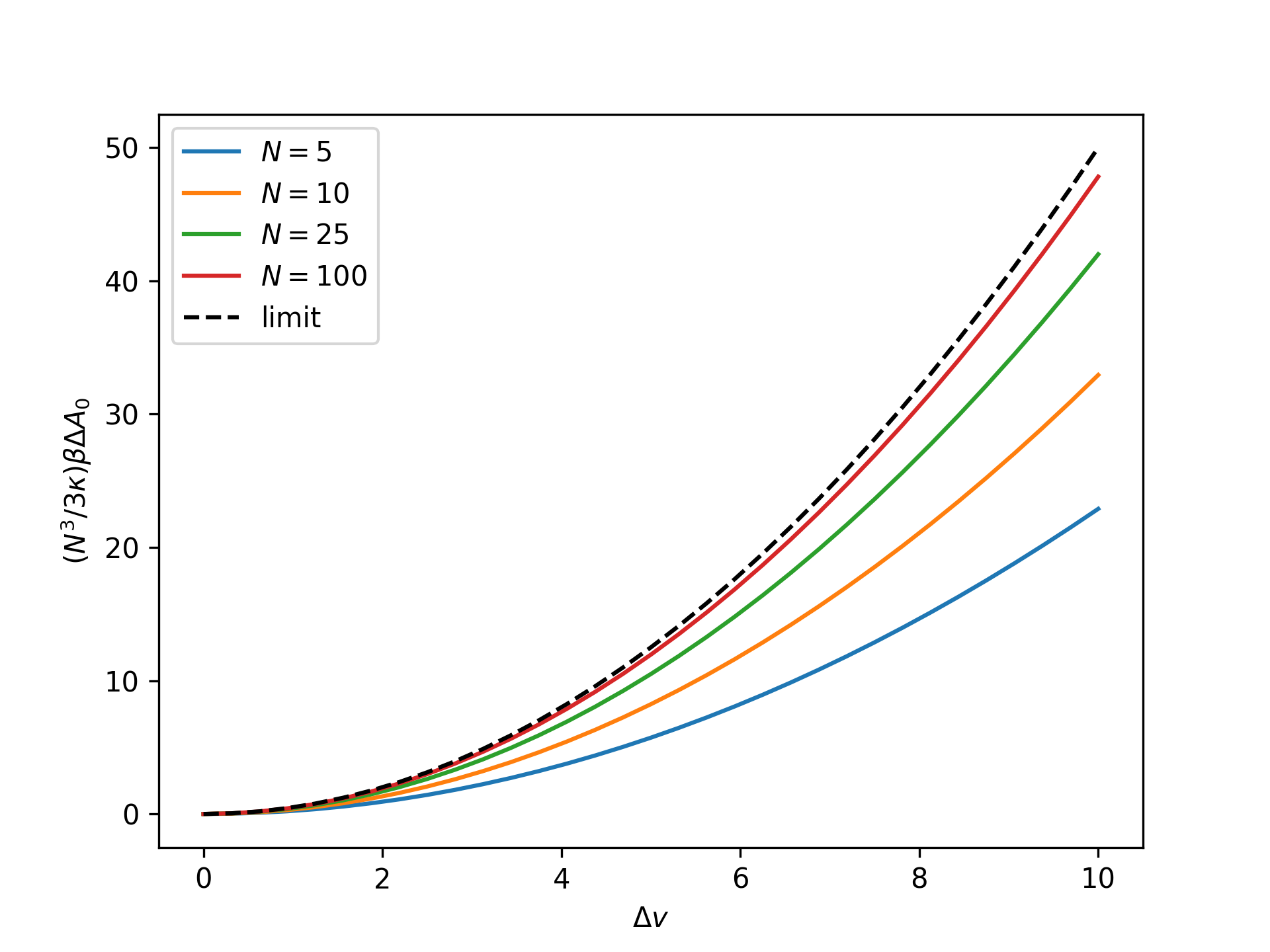
Plot the rescaled nondimensional relative Helmholtz free energy as a function of the nondimensional end separation for the reference system in the isometric ensemble for an increasing number of broken bonds \(N\) and compare to the thermodynamic limit:

>>> import numpy as np
>>> import matplotlib.pyplot as plt
>>> from statmechcrack import CrackIsometric
>>> v = np.linspace(1, 11, 33)
>>> _ = plt.figure()
>>> for N in [5, 10, 25, 100]:
...     model = CrackIsometric(N=N)
...     beta_A_0 = model.beta_A_0_isometric(v, [1, 1])
...     _ = plt.plot(v - 1, N**3/3/model.kappa*beta_A_0,
...                  label='$N=$'+str(N))
>>> _ = plt.plot(v - 1, (v - 1)**2/2, 'k--', label='limit')
>>> _ = plt.xlabel(r'$\Delta v$')
>>> _ = plt.ylabel(r'$(N^3/3\kappa)\beta\Delta A_0$')
>>> _ = plt.legend()
>>> plt.show()
_images/statmechcrack-isometric-3.png
beta_A_abs_isometric(v, approach='asymptotic', transition_state=False)[source]

The absolute nondimensional Helmholtz free energy as a function of the nondimensional end separation,

\[\beta A(v) = -\ln Q(v).\]
Parameters:

  • v (array_like) – The nondimensional end separation.

  • approach (str, optional, default='asymptotic') – The calculation approach.

  • transition_state (bool, optional, default=False) – Whether or not to calculate in the transition state.

Returns:

The absolute nondimensional Helmholtz free energy.

Return type:

numpy.ndarray

beta_A_b_isometric(v, lambda_)[source]

The relative nondimensional Helmholtz free energy as a function of the nondimensional end separation for the isolated bending system,

\[\beta\Delta A_b(v,\lambda_1,\lambda_2) = \beta A_b(v,\lambda_1,\lambda_2) - \beta A_b(v_0,\lambda_1,\lambda_2).\]

In the thermodynamic limit of a large number of broken bonds \(N\), this function has the asymptotic relation

\[\beta\Delta A_b(v,\lambda_1,\lambda_2) \sim \frac{3\kappa}{2N^3}(v - v_0)^2 \quad\text{for }N\gg 1.\]
Parameters:

  • v (array_like) – The nondimensional end separation.

  • lambda (array_like) – The intact bond stretches.

Returns:

The relative nondimensional Helmholtz free energy.

Return type:

numpy.ndarray

beta_A_b_isometric_abs(v, lambda_)[source]

The absolute nondimensional Helmholtz free energy as a function of the nondimensional end separation for the isolated bending system,

\[\beta A_b(v,\lambda_1,\lambda_2) = -\ln Q_b(v,\lambda_1,\lambda_2).\]
Parameters:

  • v (array_like) – The nondimensional end separation.

  • lambda (array_like) – The intact bond stretches.

Returns:

The absolute nondimensional Helmholtz free energy.

Return type:

numpy.ndarray

beta_A_isometric(v, approach='asymptotic', **kwargs)[source]

The relative nondimensional Helmholtz free energy as a function of the nondimensional end separation,

\[\beta\Delta A(v) = \beta A(v) - \beta A(1).\]
Parameters:

  • v (array_like) – The nondimensional end separation.

  • approach (str, optional, default='asymptotic') – The calculation approach.

  • **kwargs – Arbitrary keyword arguments. Passed to beta_A_isometric_monte_carlo().

Returns:

The relative nondimensional Helmholtz free energy.

Return type:

numpy.ndarray

Example

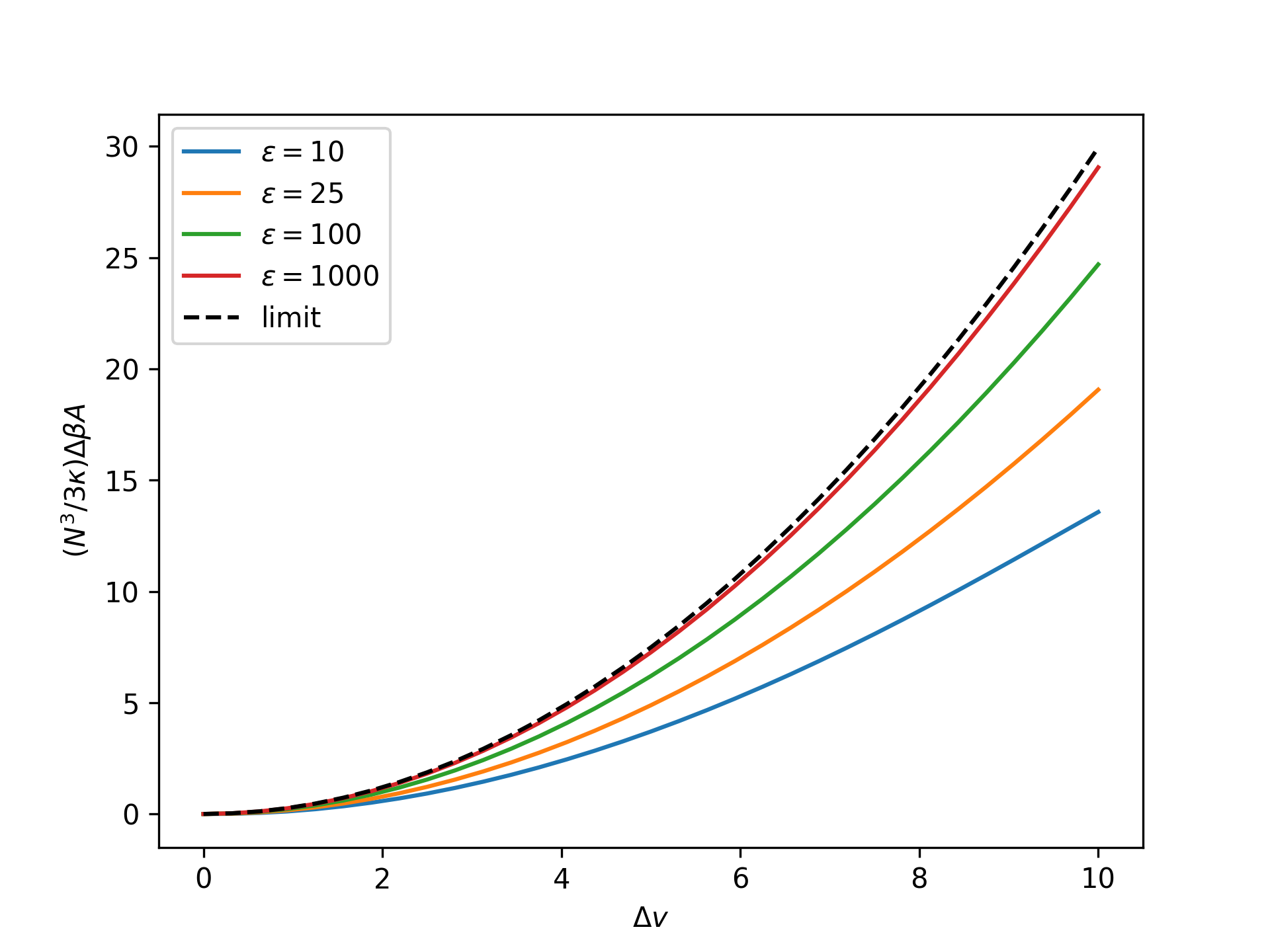
Plot the rescaled nondimensional relative Helmholtz free energy as a function of the nondimensional end separation in the isometric ensemble for an increasing nondimensional bond energy and compare to the limit given by the reference system:

>>> import numpy as np
>>> import matplotlib.pyplot as plt
>>> from statmechcrack import CrackIsometric
>>> v = np.linspace(1, 11, 33)
>>> _ = plt.figure()
>>> for varepsilon in [10, 25, 100, 1000]:
...     model = CrackIsometric(varepsilon=varepsilon)
...     beta_A = \
...         model.beta_A_isometric(v, approach='asymptotic')
...     _ = plt.plot(v - 1, model.N**3/3/model.kappa*beta_A,
...                  label=r'$\varepsilon=$'+str(varepsilon))
>>> beta_A_0 = model.beta_A_0_isometric(v, [1, 1])
>>> _ = plt.plot(v - 1, model.N**3/3/model.kappa*beta_A_0,
...              'k--', label='limit')
>>> _ = plt.xlabel(r'$\Delta v$')
>>> _ = plt.ylabel(r'$(N^3/3\kappa)\Delta\beta A$')
>>> _ = plt.legend()
>>> plt.show()
_images/statmechcrack-isometric-4.png
k_0_isometric(v, lambda_)[source]

The nondimensional forward reaction rate coefficient as a function of the nondimensional end separation for the reference system in the isometric ensemble.

Parameters:

  • v (array_like) – The nondimensional end separation.

  • lambda (array_like) – The intact bond stretches.

Returns:

The nondimensional forward reaction rate.

Return type:

numpy.ndarray

k_b_isometric(v, lambda_)[source]

The nondimensional forward reaction rate coefficient as a function of the nondimensional end separation for the isolated bending system in the isometric ensemble.

Parameters:

  • v (array_like) – The nondimensional end separation.

  • lambda (array_like) – The intact bond stretches.

Returns:

The nondimensional forward reaction rate.

Return type:

numpy.ndarray

k_isometric(v, approach='asymptotic', **kwargs)[source]

The nondimensional forward reaction rate coefficient as a function of the nondimensional end separation in the isometric ensemble.

Parameters:

  • v (array_like) – The nondimensional end separation.

  • approach (str, optional, default='asymptotic') – The calculation approach.

  • **kwargs – Arbitrary keyword arguments. Passed to k_isometric_monte_carlo().

Returns:

The nondimensional forward reaction rate.

Return type:

numpy.ndarray

Example

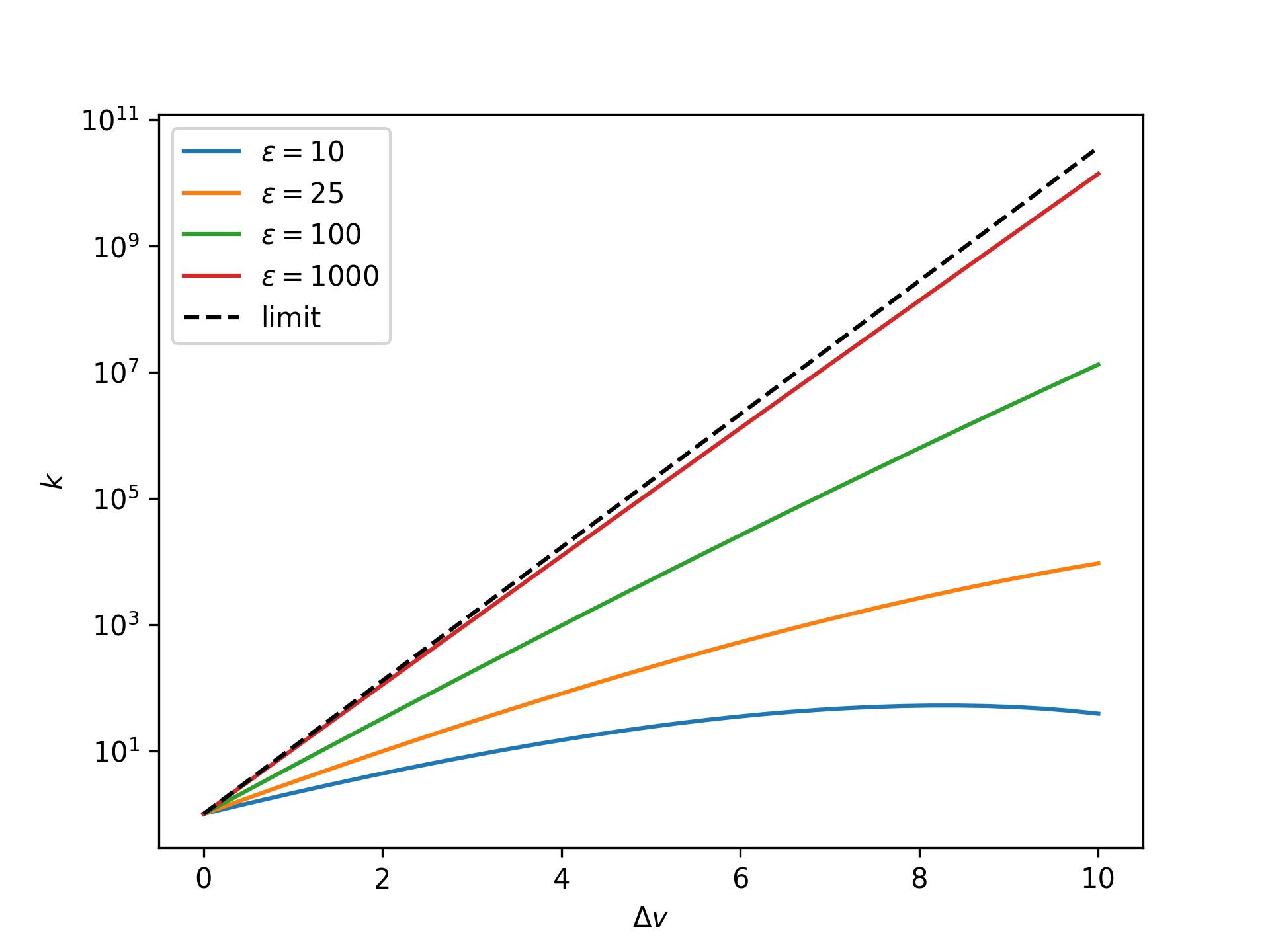
Plot the nondimensional forward reaction rate coefficient as a function of the nondimensional end separation in the isometric ensemble for an increasing nondimensional bond energy and compare to the limit given by the reference system:

>>> import numpy as np
>>> import matplotlib.pyplot as plt
>>> from statmechcrack import CrackIsometric
>>> v = np.linspace(1, 11, 33)
>>> _ = plt.figure()
>>> for varepsilon in [10, 25, 100, 1000]:
...     model = CrackIsometric(varepsilon=varepsilon)
...     _ = plt.semilogy(
...         v - 1, model.k_isometric(v),
...         label=r'$\varepsilon=$'+str(varepsilon))
>>> _ = plt.semilogy(v - 1, model.k_0_isometric(v, [1, 1]),
...                  'k--', label='limit')
>>> _ = plt.xlabel(r'$\Delta v$')
>>> _ = plt.ylabel(r'$k$')
>>> _ = plt.legend()
>>> plt.show()
_images/statmechcrack-isometric-5.png
k_net_isometric(v)[source]

The nondimensional net reaction rate coefficient as a function of the nondimensional end separation in the isometric ensemble.

Parameters:

v (array_like) – The nondimensional end separation.

Returns:

The nondimensional net reaction rate.

Return type:

numpy.ndarray

Example

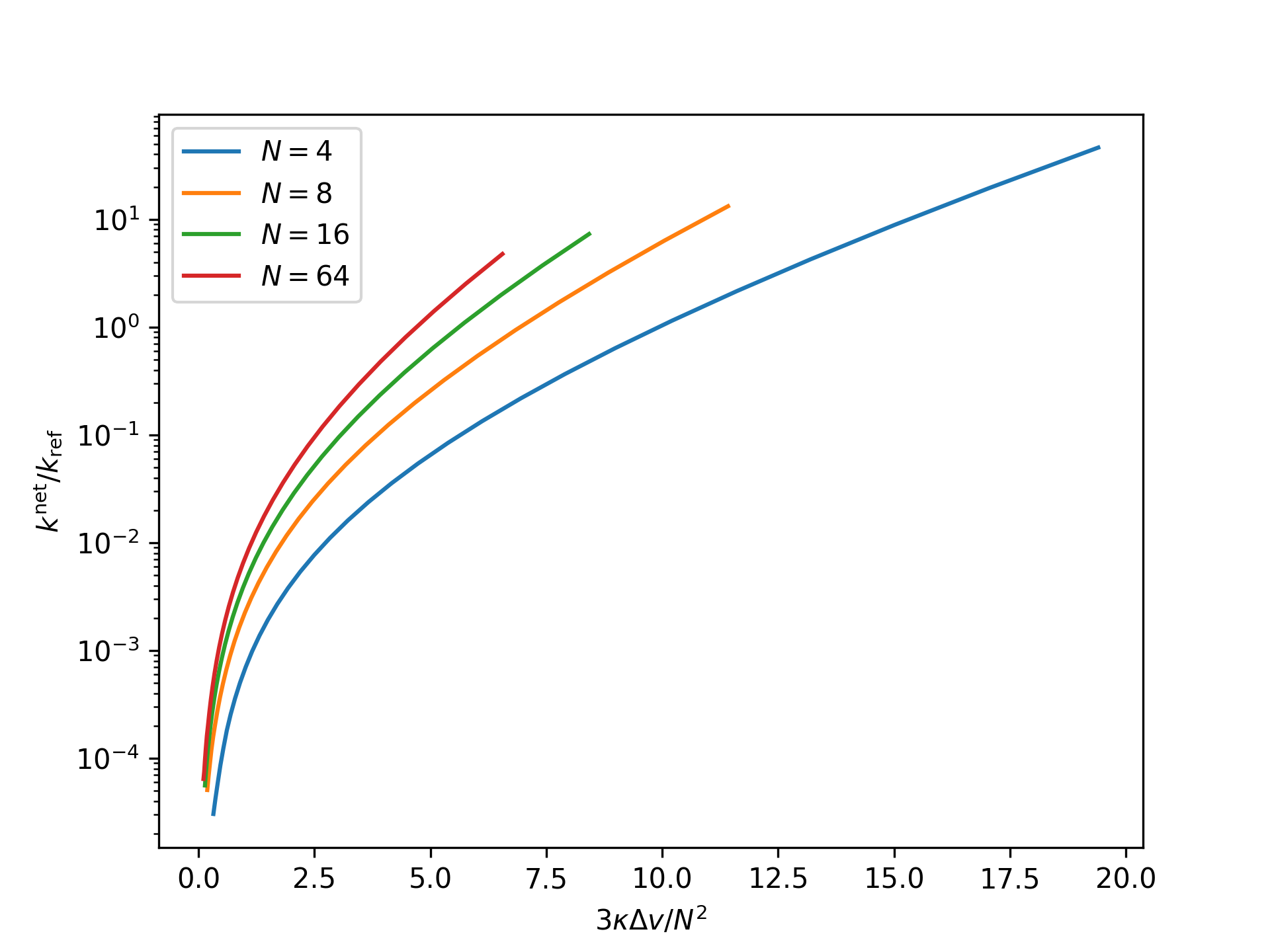
Plot the nondimensional net reaction rate coefficient as a function of the nondimensional end separation in the isometric ensemble for an increasing system size:

>>> import numpy as np
>>> import matplotlib.pyplot as plt
>>> from statmechcrack import Crack
>>> Np = np.logspace(-1, np.log(6)/np.log(10), 33)
>>> _ = plt.figure()
>>> for N in [4, 8, 16, 64]:
...     model = Crack(N=N)
...     v = model.v(Np/N, ensemble='isometric')
...     _ = plt.semilogy(
...         3*model.kappa*(v - 1)/N**2,
...         model.k_net(v, ensemble='isometric'),
...         label=r'$N=$'+str(N))
>>> _ = plt.xlabel(r'$3\kappa\Delta v/N^2$')
>>> _ = plt.ylabel(r'$k^\mathrm{net}/k_\mathrm{ref}$')
>>> _ = plt.legend()
>>> plt.show()
_images/statmechcrack-isometric-6.png
k_rev_isometric(v)[source]

The nondimensional reverse reaction rate coefficient as a function of the nondimensional end separation in the isometric ensemble.

Parameters:

v (array_like) – The nondimensional end separation.

Returns:

The nondimensional reverse reaction rate.

Return type:

numpy.ndarray

p_0_isometric(v, lambda_)[source]

The nondimensional end force as a function of the nondimensional end separation for the reference system in the isometric ensemble,

\[p_0(v,\lambda_1,\lambda_2) = \frac{\partial}{\partial v}\,\beta A_0(v,\lambda_1,\lambda_2) = p_b(v,\boldsymbol{\lambda}).\]
Parameters:

  • v (array_like) – The nondimensional end separation.

  • lambda (array_like) – The intact bond stretches.

Returns:

The nondimensional end force.

Return type:

numpy.ndarray

Example

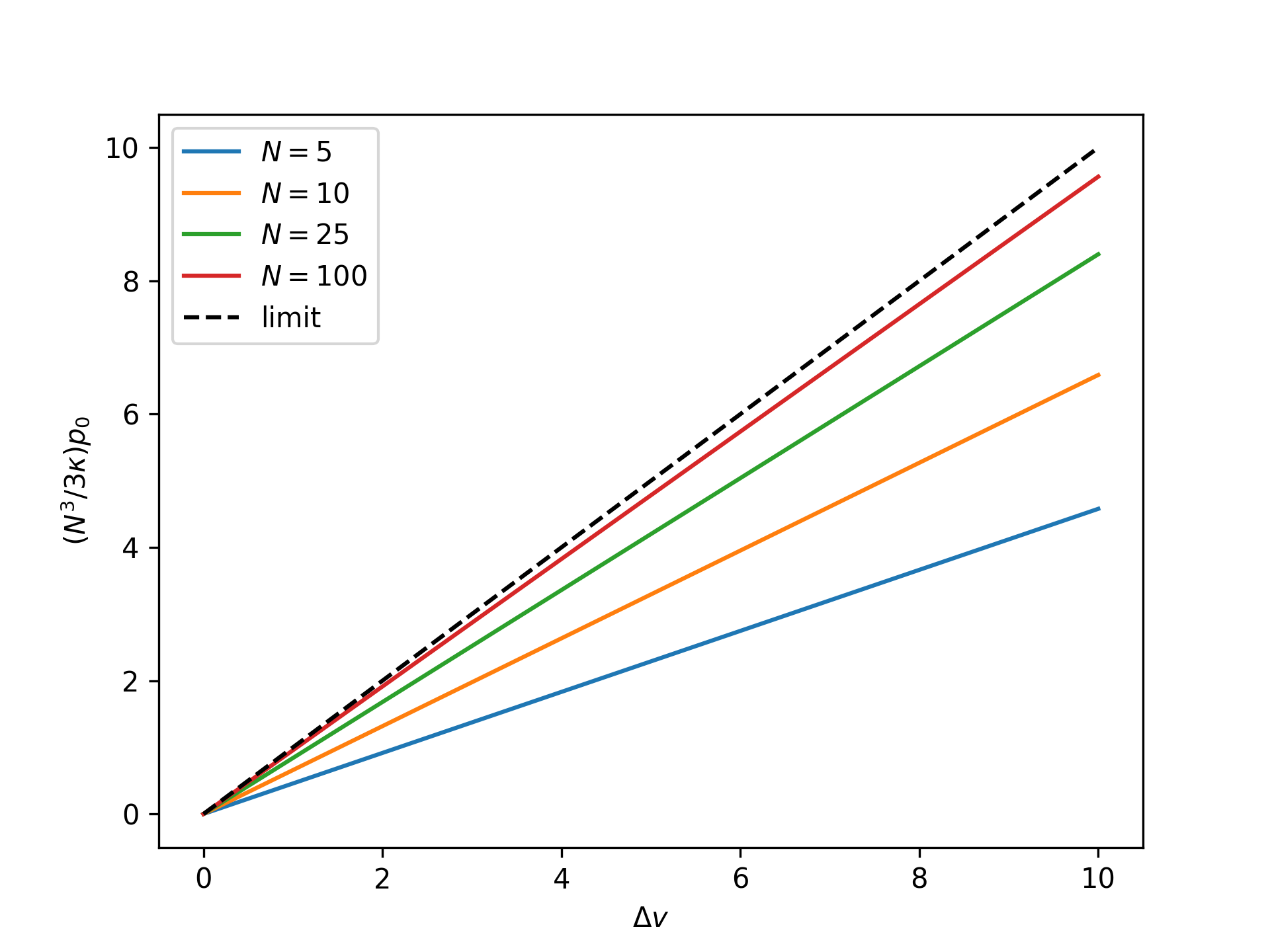
Plot the rescaled nondimensional end force as a function of the nondimensional end separation for the reference system in the isometric ensemble for an increasing number of broken bonds \(N\) and compare to the thermodynamic limit:

>>> import numpy as np
>>> import matplotlib.pyplot as plt
>>> from statmechcrack import CrackIsometric
>>> v = np.linspace(1, 11, 33)
>>> _ = plt.figure()
>>> for N in [5, 10, 25, 100]:
...     model = CrackIsometric(N=N)
...     p_0 = model.p_0_isometric(v, [1, 1])
...     _ = plt.plot(v - 1, N**3/3/model.kappa*p_0,
...                  label='$N=$'+str(N))
>>> _ = plt.plot(v - 1, v - 1, 'k--', label='limit')
>>> _ = plt.xlabel(r'$\Delta v$')
>>> _ = plt.ylabel(r'$(N^3/3\kappa)p_0$')
>>> _ = plt.legend()
>>> plt.show()
_images/statmechcrack-isometric-7.png
p_b_isometric(v, lambda_)[source]

The nondimensional end force as a function of the nondimensional end separation for the isolated bending system in the isometric ensemble,

\[p_b(v,\lambda_1,\lambda_2) = \frac{\partial}{\partial v}\,\beta A_b(v,\lambda_1,\lambda_2).\]

In the thermodynamic limit of a large number of broken bonds \(N\), this function has the asymptotic relation

\[p_b(v,\lambda_1,\lambda_2) \sim \frac{3\kappa}{N^3}(v - v_0) \quad\text{for }N\gg 1.\]
Parameters:

  • v (array_like) – The nondimensional end separation.

  • lambda (array_like) – The intact bond stretches.

Returns:

The nondimensional end force.

Return type:

numpy.ndarray

p_isometric(v, approach='asymptotic', **kwargs)[source]

The nondimensional end force as a function of the nondimensional end separation in the isometric ensemble,

\[p(v) = \frac{\partial}{\partial v}\,\beta A(v).\]
Parameters:

  • v (array_like) – The nondimensional end separation.

  • approach (str, optional, default='asymptotic') – The calculation approach.

  • **kwargs – Arbitrary keyword arguments. Passed to p_isometric_monte_carlo().

Returns:

The nondimensional end force.

Return type:

numpy.ndarray

Example

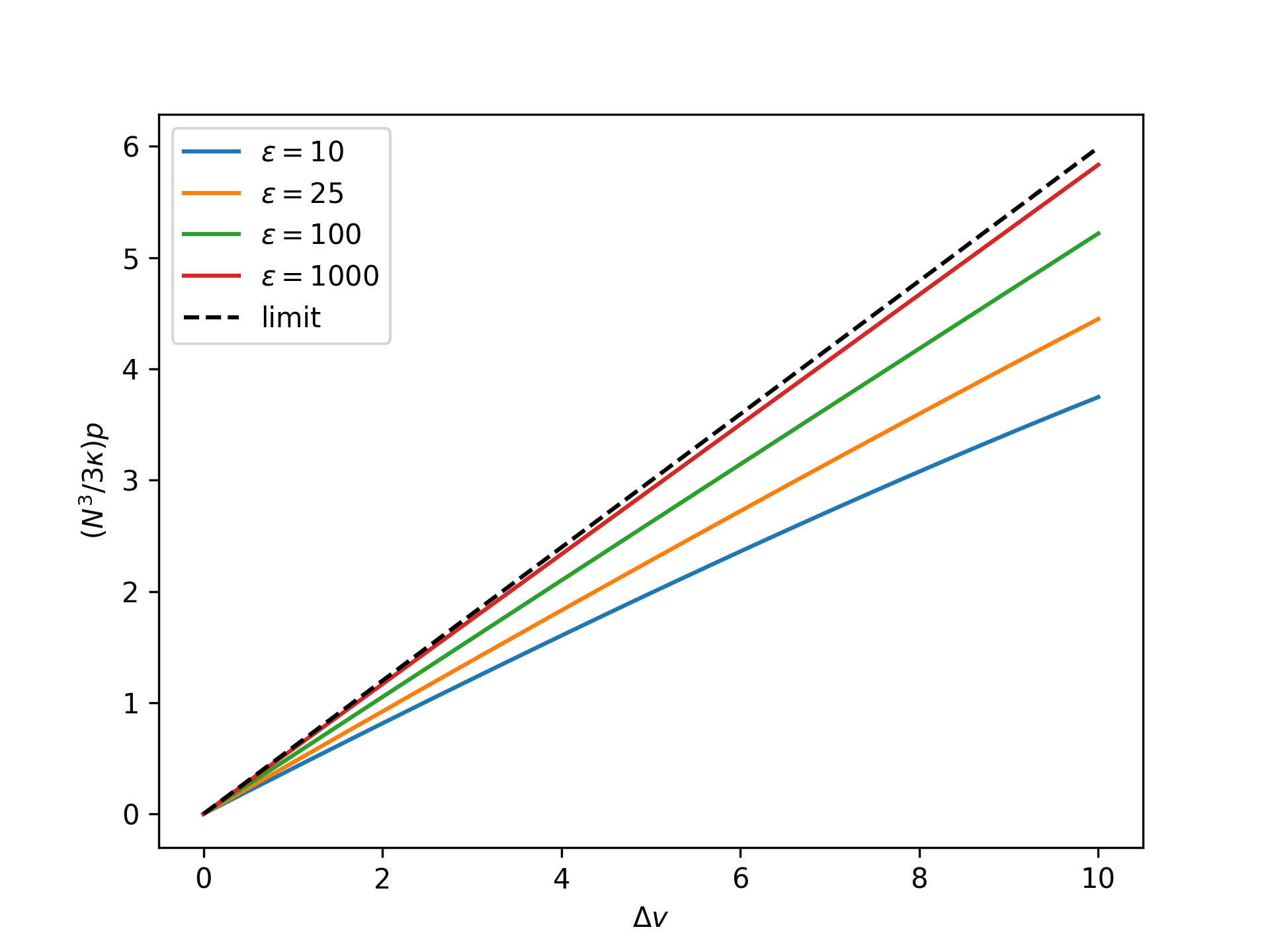
Plot the rescaled nondimensional end force as a function of the nondimensional end separation in the isometric ensemble for an increasing nondimensional bond energy and compare to the limit given by the reference system:

>>> import numpy as np
>>> import matplotlib.pyplot as plt
>>> from statmechcrack import CrackIsometric
>>> v = np.linspace(1, 11, 33)
>>> _ = plt.figure()
>>> for varepsilon in [10, 25, 100, 1000]:
...     model = CrackIsometric(varepsilon=varepsilon)
...     p = model.p_isometric(v, approach='asymptotic')
...     _ = plt.plot(v - 1, model.N**3/3/model.kappa*p,
...                  label=r'$\varepsilon=$'+str(varepsilon))
>>> p_0 = model.p_0_isometric(v, [1, 1])
>>> _ = plt.plot(v - 1, model.N**3/3/model.kappa*p_0,
...              'k--', label='limit')
>>> _ = plt.xlabel(r'$\Delta v$')
>>> _ = plt.ylabel(r'$(N^3/3\kappa)p$')
>>> _ = plt.legend()
>>> plt.show()
_images/statmechcrack-isometric-8.png