statmechcrack.mechanical
A module for the crack model treated mechanically.
This module consist of the class CrackMechanical which
contains methods for computing quantities when treating
the crack model mechanically rather than statistical mechanically.
- class CrackMechanical(N=8, M=8, kappa=100, alpha=1, varepsilon=100)[source]
Bases:
BasicUtilityThe crack model class treated mechanically.
- N
The number of broken bonds.
- Type:
int
- M
The number of intact bonds.
- Type:
int
- L
The total number of bonds.
- Type:
int
- kappa
The nondimensional bending stiffness.
- Type:
float
- alpha
The nondimensional Morse parameter.
- Type:
float
- varepsilon
The nondimensional bond energy.
- Type:
float
- H_Pi(s)[source]
The nondimensional Hessian of the total potential energy of the system,
\[\mathbf{H}^\Pi(\mathbf{s}) = \mathbf{H}^\Pi_0 +\mathbf{H}^\Pi_1(\boldsymbol{\lambda}).\]where \(\lambda_j\equiv s_{N+j}\) and \(j=1,\ldots,M\).
- Parameters:
s (array_like) – The nondimensional configuration.
- Returns:
The nondimensional Hessian.
- Return type:
numpy.ndarray
- H_Pi_0()[source]
The nondimensional Hessian of the total potential energy of the system due to bending,
\[\begin{split}\left[\mathbf{H}^\Pi_0\right]_{mn} = \kappa\left(\phantom{\delta^{|m-n|}_1}\right. & 6\delta^m_n - 5\delta^m_1\delta^n_1 - \delta^m_2\delta^n_2 - 5\delta^m_{L+1}\delta^n_{L+1} - \delta^m_L\delta^n_L - 4\delta^{|m-n|}_1 \\ & + 2\delta^m_1\delta^n_2 + 2\delta^m_2\delta^n_1 + 2\delta^m_{L+1}\delta^n_L + 2\delta^m_L\delta^n_{L+1} + \delta^{|m-n|}_2 \left.\phantom{\delta^{|m-n|}_1}\right), \\ & \quad m,n=1,\ldots,L+1.\end{split}\]- Returns:
The nondimensional Hessian.
- Return type:
numpy.ndarray
- H_Pi_00()[source]
The nondimensional Hessian of the total potential energy for the isolated bending system,
\[\begin{split}\left[\mathbf{H}^\Pi_b\right]_{mn} = \kappa\left(\phantom{\delta^{|m-n|}_1}\right. & 6\delta^m_n - 5\delta^m_1\delta^n_1 - \delta^m_2\delta^n_2 - 4\delta^{|m-n|}_1 \\ & + 2\delta^m_1\delta^n_2 + 2\delta^m_2\delta^n_1 + \delta^{|m-n|}_2 \left.\phantom{\delta^{|m-n|}_1}\right), \quad m,n=1,\ldots,N+1.\end{split}\]- Returns:
The nondimensional Hessian.
- Return type:
numpy.ndarray
- H_Pi_1(lambda_)[source]
The nondimensional Hessian of the total potential energy of the system due to stretching intact bonds,
\[\left[\mathbf{H}^\Pi_1(\boldsymbol{\lambda})\right]_{mn} = \left[\mathbf{H}^U_1(\boldsymbol{\lambda})\right]_{mn}.\]- Parameters:
lambda (array_like) – The intact bond stretches.
- Returns:
The nondimensional Hessian.
- Return type:
numpy.ndarray
- H_Pi_TS(s)[source]
The nondimensional Hessian of the total potential energy of the system in its transition state.
- Parameters:
s (array_like) – The nondimensional configuration.
- Returns:
The nondimensional Hessian.
- Return type:
numpy.ndarray
- H_U(s)[source]
The nondimensional Hessian of the potential energy of the system,
\[\mathbf{H}^U(\mathbf{s}) = \mathbf{H}^U_0 +\mathbf{H}^U_1(\boldsymbol{\lambda}).\]where \(\lambda_j\equiv s_{N+j}\) and \(j=1,\ldots,M\).
- Parameters:
s (array_like) – The nondimensional configuration.
- Returns:
The nondimensional Hessian.
- Return type:
numpy.ndarray
- H_U_0()[source]
The nondimensional Hessian of the potential energy of the system due to bending,
\[\left[\mathbf{H}^U_0\right]_{mn} = \left[\mathbf{H}^\pi_0\right]_{m+1,n+1}, \quad m,n=1,\ldots,L.\]- Returns:
The nondimensional Hessian.
- Return type:
numpy.ndarray
- H_U_00()[source]
The nondimensional Hessian of the potential energy for the isolated bending system,
\[\left[\mathbf{H}^U_00\right]_{mn} = \kappa\left(6\delta^m_n - \delta^m_1\delta^n_1 - 4\delta^{|m-n|}_1 + \delta^{|m-n|}_2\right), \quad m,n=1,\ldots,N.\]- Returns:
The nondimensional Hessian.
- Return type:
numpy.ndarray
- H_U_1(lambda_)[source]
The nondimensional Hessian of the potential energy of the system due to stretching intact bonds,
\[\left[\mathbf{H}^U_1(\boldsymbol{\lambda})\right]_{mn} = 2\alpha^2\varepsilon e^{-\alpha(\lambda_m-1)}\left( 1 - 2e^{-\alpha(\lambda_m-1)} \right)\delta^m_n.\]- Parameters:
lambda (array_like) – The intact bond stretches.
- Returns:
The nondimensional Hessian.
- Return type:
numpy.ndarray
- H_U_TS(s)[source]
The nondimensional Hessian of the potential energy of the system in its transition state.
- Parameters:
s (array_like) – The nondimensional configuration.
- Returns:
The nondimensional Hessian.
- Return type:
numpy.ndarray
- beta_Pi(p, v, s)[source]
The nondimensional total potential energy of the system,
\[\beta \Pi(p,v,\mathbf{s}) = \beta U(v,\mathbf{s}) - pv.\]- Parameters:
p (array_like) – The nondimensional end force.
v (array_like) – The nondimensional end separation.
s (array_like) – The nondimensional configuration.
- Returns:
The nondimensional total potential energy.
- Return type:
numpy.ndarray
- beta_Pi_0(p, v, s)[source]
The nondimensional total potential energy of the reference system,
\[\beta \Pi_{0}(p,v,\mathbf{s}) = \beta U_{0}(v,\mathbf{s}) - pv.\]- Parameters:
p (array_like) – The nondimensional end force.
v (array_like) – The nondimensional end separation.
s (array_like) – The nondimensional configuration.
- beta_Pi_00(p, v, s)[source]
The nondimensional total potential energy for the isolated bending system,
\[\beta \Pi_b(p,v,\mathbf{s}) = \beta U_{00}(v,\mathbf{s}) - pv.\]- Parameters:
p (array_like) – The nondimensional end force.
v (array_like) – The nondimensional end separation.
s (array_like) – The nondimensional configuration.
- beta_U(v, s)[source]
The nondimensional potential energy of the system,
\[\beta U(v,\mathbf{s}) = \beta U_0(v,\mathbf{s}) + \beta U_1(\boldsymbol{\lambda}),\]where \(\lambda_j\equiv s_{N+j}\) and \(j=1,\ldots,M\).
- Parameters:
v (array_like) – The nondimensional end separation.
s (array_like) – The nondimensional configuration.
- Returns:
The nondimensional potential energy.
- Return type:
numpy.ndarray
- beta_U_0(v, s)[source]
The nondimensional potential energy of the system due to bending, i.e. of the reference system,
\[\beta U_0(v, \mathbf{s}) = \sum_{i=1}^{L-1} \frac{\kappa}{2} \left( s_{i-1} - 2s_i + s_{i+1} \right)^2,\]where \(s_0\equiv v\).
- Parameters:
v (array_like) – The nondimensional end separation.
s (array_like) – The nondimensional configuration.
- Returns:
The nondimensional potential energy.
- Return type:
numpy.ndarray
- beta_U_00(v, s)[source]
The nondimensional potential energy of the isolated bending system,
\[\beta U_{00}(v, \mathbf{s}) = \sum_{i=1}^{N+1} \frac{\kappa}{2} \left( s_{i-1} - 2s_i + s_{i+1} \right)^2,\]where \(s_0\equiv v\), and \(s_{N+1}\equiv\lambda_1\), and \(s_{N+2}\equiv\lambda_2\).
- Parameters:
v (array_like) – The nondimensional end separation.
s (array_like) – The nondimensional configuration.
- Returns:
The nondimensional potential energy.
- Return type:
numpy.ndarray
- beta_U_01(lambda_)[source]
The nondimensional potential energy due to bending within the intact region,
\[\begin{split}\beta U_{01}(\boldsymbol{\lambda}) &= \beta U_0(v, \mathbf{s}) - \beta U_{00}(v, \mathbf{s}) \\ &= \sum_{i=N+2}^{L-1} \frac{\kappa}{2} \left( s_{i-1} - 2s_i + s_{i+1} \right)^2 \\ &= \sum_{j=2}^{M-1} \frac{\kappa}{2} \left( \lambda_{j-1} - 2\lambda_j + \lambda_{j+1} \right)^2,\end{split}\]where \(s_0\equiv v\), and \(s_{N+1}\equiv\lambda_1\), and \(s_{N+2}\equiv\lambda_2\).
- Parameters:
lambda (array_like) – The intact bond stretches.
- Returns:
The nondimensional potential energy.
- Return type:
numpy.ndarray
- beta_U_1(lambda_)[source]
The nondimensional potential energy of the system due to stretching intact bonds,
\[\beta U_1(\boldsymbol{\lambda}) = \sum_{j=1}^M \varepsilon\beta u(\lambda_j).\]- Parameters:
lambda (array_like) – The intact bond stretches.
- Returns:
The nondimensional potential energy.
- Return type:
numpy.ndarray
- beta_u(lambda_)[source]
The nondimensional potential energy of a single bond as a function of the bond stretch, given by the Morse potential [1],
\[\beta u(\lambda) = \varepsilon \left[ 1 - e^{-\alpha(\lambda - 1)} \right]^2.\]- Parameters:
lambda (array_like) – The bond stretch.
- Returns:
The nondimensional potential energy.
- Return type:
numpy.ndarray
- beta_u_p(lambda_)[source]
The first derivative of the potential energy of a single bond as a function of the bond stretch,
\[\beta u'(\lambda) = 2\alpha\varepsilon e^{-\alpha(\lambda - 1)} \left[ 1 - e^{-\alpha(\lambda - 1)} \right]^2.\]- Parameters:
lambda (array_like) – The bond stretch.
- Returns:
The first derivative of the nondimensional potential energy.
- Return type:
numpy.ndarray
- beta_u_pp(lambda_)[source]
The second derivative of the potential energy of a single bond as a function of the bond stretch,
\[\beta u''(\lambda) = 2\alpha^2\varepsilon e^{-\alpha(\lambda - 1)} \left[ 2e^{-\alpha(\lambda - 1)} - 1 \right]^2.\]- Parameters:
lambda (array_like) – The bond stretch.
- Returns:
The second derivative of the nondimensional potential energy.
- Return type:
numpy.ndarray
- j_Pi(p, v, s)[source]
The nondimensional Jacobian of the total potential energy of the system,
\[\mathbf{j}^\Pi(p,v,\mathbf{s}) = \mathbf{j}^\Pi_0(p,v,\mathbf{s}) +\mathbf{j}^\Pi_1(\boldsymbol{\lambda}).\]where \(\lambda_j\equiv s_{N+j}\) and \(j=1,\ldots,M\).
- Parameters:
p (array_like) – The nondimensional end force.
v (array_like) – The nondimensional end separation.
s (array_like) – The nondimensional configuration.
- Returns:
The nondimensional Jacobian.
- Return type:
numpy.ndarray
- j_Pi_0(p, v, s)[source]
The nondimensional Jacobian of the total potential energy of the system due to bending,
\[\mathbf{j}^\Pi_0(p,v,\mathbf{s}) = \mathbf{H}^\Pi_0 \cdot \left( v, s_1, \cdots, s_L \right)^T - \left( p, 0, \ldots, 0 \right)^T\]- Parameters:
p (array_like) – The nondimensional end force.
v (array_like) – The nondimensional end separation.
s (array_like) – The nondimensional configuration.
- Returns:
The nondimensional Jacobian.
- Return type:
numpy.ndarray
- j_Pi_00(p, v, s)[source]
The nondimensional Jacobian of the total potential energy of the system for the isolated bending system,
\[\mathbf{j}^\Pi_b(p,v,\mathbf{s}) = \mathbf{H}^\Pi_b \cdot \left( v, s_1, \cdots, s_N \right)^T - \kappa\left( p/\kappa, 0, \ldots, 0, -\lambda_1, 4\lambda_1-\lambda_2 \right)^T\]- Parameters:
p (array_like) – The nondimensional end force.
v (array_like) – The nondimensional end separation.
s (array_like) – The nondimensional configuration.
- Returns:
The nondimensional Jacobian.
- Return type:
numpy.ndarray
- j_Pi_1(lambda_)[source]
The nondimensional Jacobian of the total potential energy of the system due to stretching intact bonds,
\[\mathbf{j}^\Pi_1(\boldsymbol{\lambda}) = \mathbf{j}^U_1(\boldsymbol{\lambda}).\]- Parameters:
lambda (array_like) – The intact bond stretches.
- Returns:
The nondimensional Jacobian.
- Return type:
numpy.ndarray
- j_Pi_TS(p, v, s)[source]
The nondimensional Jacobian of the total potential energy of the system in its transition state.
- Parameters:
p (array_like) – The nondimensional end force.
v (array_like) – The nondimensional end separation.
s (array_like) – The nondimensional configuration.
- Returns:
The nondimensional Jacobian.
- Return type:
numpy.ndarray
- j_U(v, s)[source]
The nondimensional Jacobian of the potential energy of the system,
\[\mathbf{j}^U(v,\mathbf{s}) = \mathbf{j}^U_0(v,\mathbf{s}) +\mathbf{j}^U_1(\boldsymbol{\lambda}).\]where \(\lambda_j\equiv s_{N+j}\) and \(j=1,\ldots,M\).
- Parameters:
v (array_like) – The nondimensional end separation.
s (array_like) – The nondimensional configuration.
- Returns:
The nondimensional Jacobian.
- Return type:
numpy.ndarray
- j_U_0(v, s)[source]
The nondimensional Jacobian of the potential energy of the system for the reference system,
\[\mathbf{j}^U_0(v,\mathbf{s}) = \mathbf{H}^U_0 \cdot \mathbf{s} - \kappa\left( 2v, -v, 0, \ldots, 0 \right)^T\]- Parameters:
v (array_like) – The nondimensional end separation.
s (array_like) – The nondimensional configuration.
- Returns:
The nondimensional Jacobian.
- Return type:
numpy.ndarray
- j_U_00(v, s)[source]
The nondimensional Jacobian of the potential energy of the system for the isolated bending system,
\[\mathbf{j}^U_00(v,\mathbf{s}) = \mathbf{H}^U_00 \cdot \mathbf{s} - \kappa\left( 2v, -v, 0, \ldots, 0, -\lambda_1, 4\lambda_1-\lambda_2 \right)^T.\]- Parameters:
v (array_like) – The nondimensional end separation.
s (array_like) – The nondimensional configuration.
- Returns:
The nondimensional Jacobian.
- Return type:
numpy.ndarray
- j_U_1(lambda_)[source]
The nondimensional Jacobian of the potential energy of the system due to stretching intact bonds,
\[\left[\mathbf{j}^U_1(\boldsymbol{\lambda})\right]_j = 2\alpha\varepsilon e^{-\alpha(\lambda_j-1)}\left( 1 - e^{-\alpha(\lambda_j-1)} \right).\]- Parameters:
lambda (array_like) – The intact bond stretches.
- Returns:
The nondimensional Jacobian.
- Return type:
numpy.ndarray
- j_U_TS(v, s)[source]
The nondimensional Jacobian of the potential energy of the system in its transition state.
- Parameters:
v (array_like) – The nondimensional end separation.
s (array_like) – The nondimensional configuration.
- Returns:
The nondimensional Jacobian.
- Return type:
numpy.ndarray
- minimize_beta_Pi(p, transition_state=False)[source]
Function to minimize the total potential energy of the system.
- Parameters:
p (array_like) – The nondimensional end force.
transition_state (bool, optional, default=False) – Whether or not to fix the crack tip bond stretch at the transition state stretch.
- Returns:
(numpy.ndarray) - The minimized nondimensional total potential energy.
(numpy.ndarray) - The corresponding nondimensional end separation.
(numpy.ndarray) - The corresponding nondimensional positions.
- Return type:
tuple
- minimize_beta_Pi_00(p, lambda_)[source]
Function to minimize the total potential energy of the isolated bending system.
- Parameters:
p (array_like) – The nondimensional end force.
lambda (array_like) – The intact bond stretches.
- Returns:
(numpy.ndarray) - The minimized nondimensional total potential energy.
(numpy.ndarray) - The corresponding nondimensional end separation.
(numpy.ndarray) - The corresponding nondimensional positions.
- Return type:
tuple
- minimize_beta_U(v, transition_state=False)[source]
Function to minimize the potential energy of the system.
- Parameters:
v (array_like) – The nondimensional end separation.
transition_state (bool, optional, default=False) – Whether or not to fix the crack tip bond stretch at the transition state stretch.
- Returns:
(numpy.ndarray) - The minimized nondimensional potential energy.
(numpy.ndarray) - The corresponding nondimensional positions.
- Return type:
tuple
Example
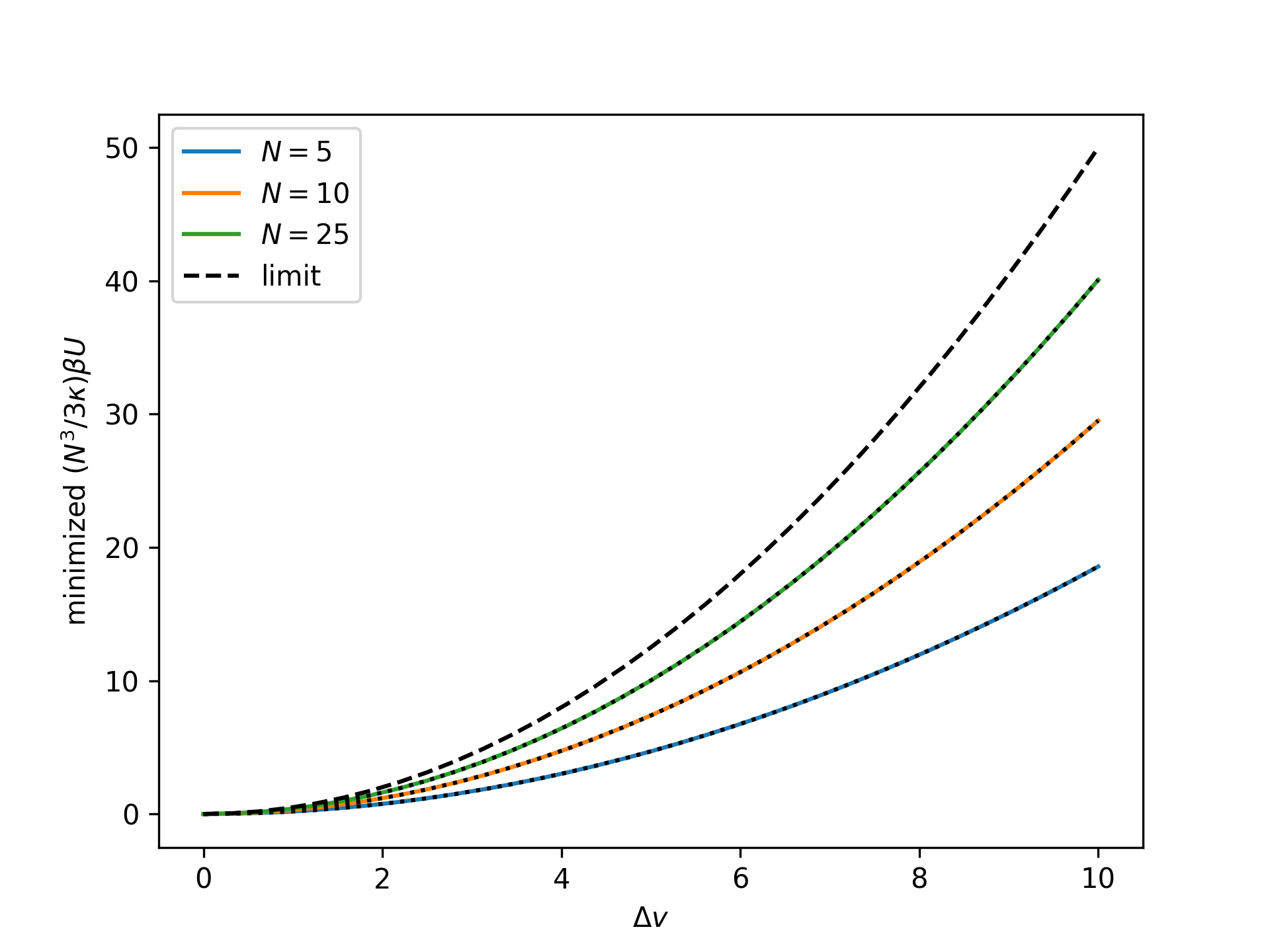
Plot the rescaled minimized nondimensional potential energy as a function of the nondimensional end separation for the mechnically-treated system for an increasing number of broken bonds \(N\) and compare to the thermodynamic limit:
>>> import numpy as np >>> import matplotlib.pyplot as plt >>> from statmechcrack import CrackMechanical >>> v = np.linspace(1, 11, 33) >>> _ = plt.figure() >>> for N in [5, 10, 25]: ... model = CrackMechanical(N=N) ... beta_U = model.minimize_beta_U(v)[0] ... _ = plt.plot(v - 1, model.N**3/3/model.kappa*beta_U, ... label='$N=$'+str(N)) ... p_m = model.p_mechanical(v) ... beta_Pi = model.minimize_beta_Pi(p_m)[0] ... _ = plt.plot(v - 1, ... model.N**3/3/model.kappa*(beta_Pi+p_m*v) ... , 'k:') >>> _ = plt.plot(v - 1, (v - 1)**2/2, 'k--', label='limit') >>> _ = plt.xlabel(r'$\Delta v$') >>> _ = plt.ylabel(r'minimized $(N^3/3\kappa)\beta U$') >>> _ = plt.legend() >>> plt.show()
- minimize_beta_U_00(v, lambda_)[source]
Function to minimize the potential energy of the isolated bending system.
- Parameters:
v (array_like) – The nondimensional end separation.
lambda (array_like) – The intact bond stretches.
- Returns:
(numpy.ndarray) - The minimized nondimensional potential energy.
(numpy.ndarray) - The corresponding nondimensional end separation.
(numpy.ndarray) - The corresponding nondimensional positions.
- Return type:
tuple
Example
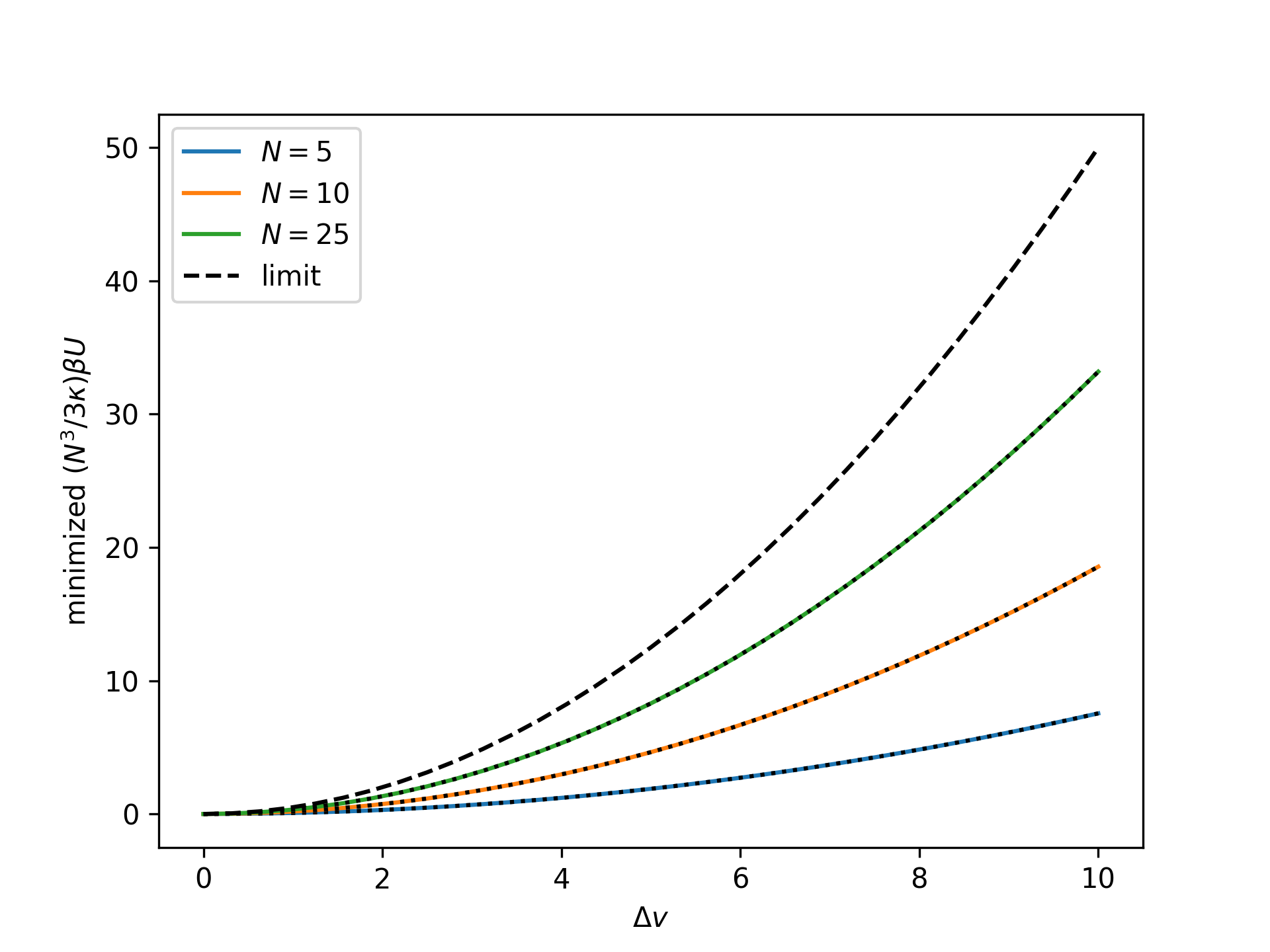
Plot the rescaled minimized nondimensional potential energy as a function of the nondimensional end separation for the mechnically-treated isolated bending system for an increasing number of broken bonds \(N\) and compare to the thermodynamic limit:
>>> import numpy as np >>> import matplotlib.pyplot as plt >>> from statmechcrack import CrackMechanical >>> v = np.linspace(1, 11, 33) >>> _ = plt.figure() >>> for N in [5, 10, 25]: ... model = CrackMechanical(N=N) ... beta_U = model.minimize_beta_U_00(v, [1, 1])[0] ... _ = plt.plot(v - 1, model.N**3/3/model.kappa*beta_U, ... label='$N=$'+str(N)) ... p_m = model.p_0_mechanical(v, [1, 1]) ... beta_Pi = model.minimize_beta_Pi_00(p_m, [1, 1])[0] ... _ = plt.plot(v - 1, ... model.N**3/3/model.kappa*(beta_Pi+p_m*v) ... , 'k:') >>> _ = plt.plot(v - 1, (v - 1)**2/2, 'k--', label='limit') >>> _ = plt.xlabel(r'$\Delta v$') >>> _ = plt.ylabel(r'minimized $(N^3/3\kappa)\beta U$') >>> _ = plt.legend() >>> plt.show()
- p_0_mechanical(v, lambda_)[source]
The nondimensional end force as a function of the nondimensional end separation for the mechnically-treated reference system, calculated by minimizing the potential energy.
- Parameters:
v (array_like) – The nondimensional end separation.
lambda (array_like) – The intact bond stretches.
- Returns:
The nondimensional end force.
- Return type:
numpy.ndarray
Example
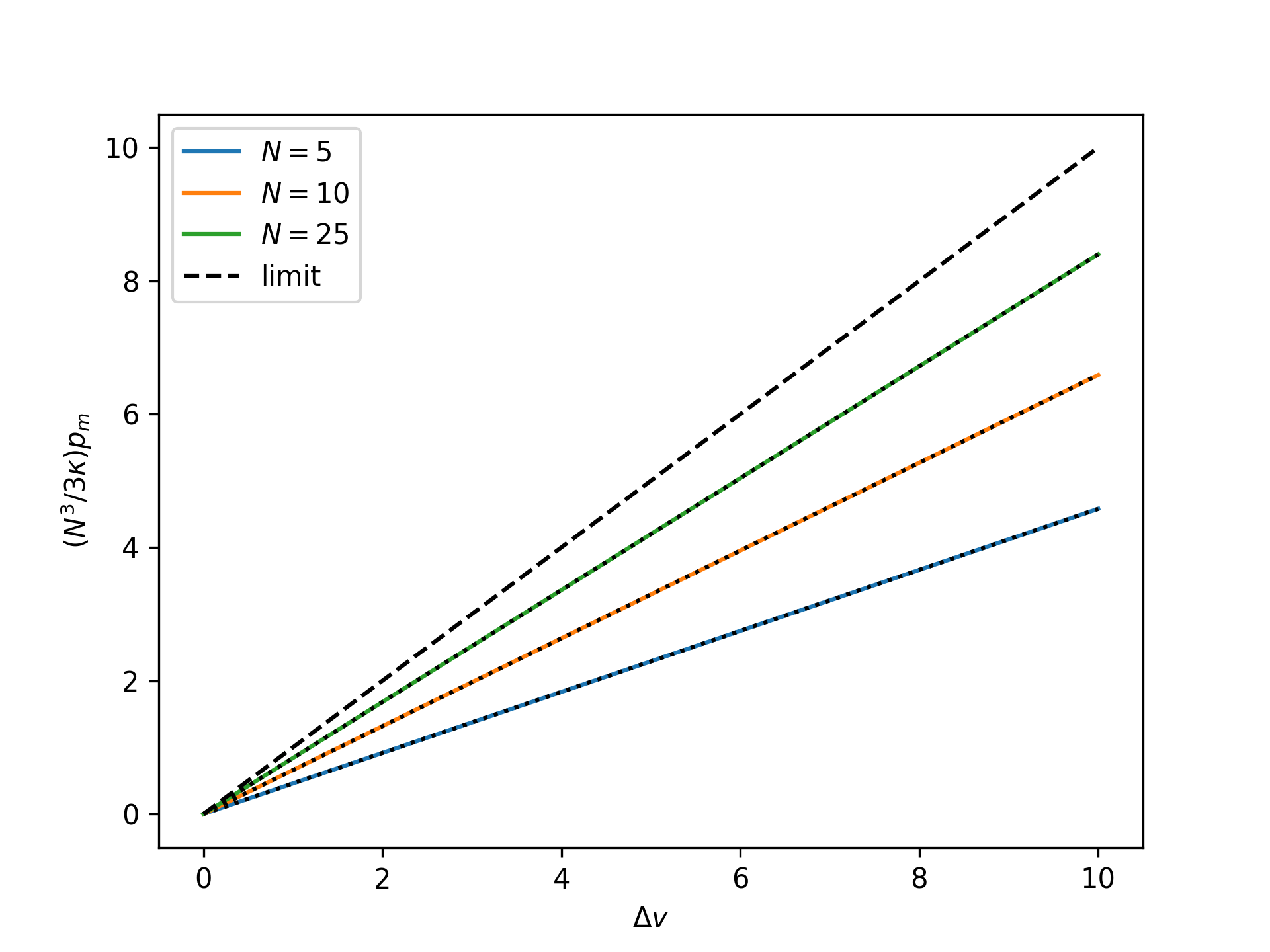
Plot the rescaled nondimensional end force as a function of the nondimensional end separation for the mechnically-treated reference system for an increasing number of broken bonds \(N\) and compare to the thermodynamic limit:
>>> import numpy as np >>> import matplotlib.pyplot as plt >>> from statmechcrack import CrackMechanical >>> v = np.linspace(1, 11, 33) >>> _ = plt.figure() >>> for N in [5, 10, 25]: ... model = CrackMechanical(N=N) ... p_m = model.p_0_mechanical(v, [1, 1]) ... r_p_m = model.N**3/3/model.kappa*p_m ... _ = plt.plot(v - 1, r_p_m, label='$N=$'+str(N)) ... v_m = model.v_0_mechanical(p_m, [1, 1]) ... _ = plt.plot(v_m - 1, r_p_m, 'k:') >>> _ = plt.plot(v - 1, v - 1, 'k--', label='limit') >>> _ = plt.xlabel(r'$\Delta v$') >>> _ = plt.ylabel(r'$(N^3/3\kappa)p_m$') >>> _ = plt.legend() >>> plt.show()
- p_b_mechanical(v, lambda_)[source]
The nondimensional end force as a function of the nondimensional end separation for the mechnically-treated reference system, calculated by minimizing the potential energy.
- Parameters:
v (array_like) – The nondimensional end separation.
lambda (array_like) – The intact bond stretches.
- Returns:
The nondimensional end force.
- Return type:
numpy.ndarray
- p_mechanical(v)[source]
The nondimensional end force as a function of the nondimensional end separation for the mechnically-treated system, calculated by minimizing the potential energy.
- Parameters:
v (array_like) – The nondimensional end separation.
- Returns:
The nondimensional end force.
- Return type:
numpy.ndarray
Example
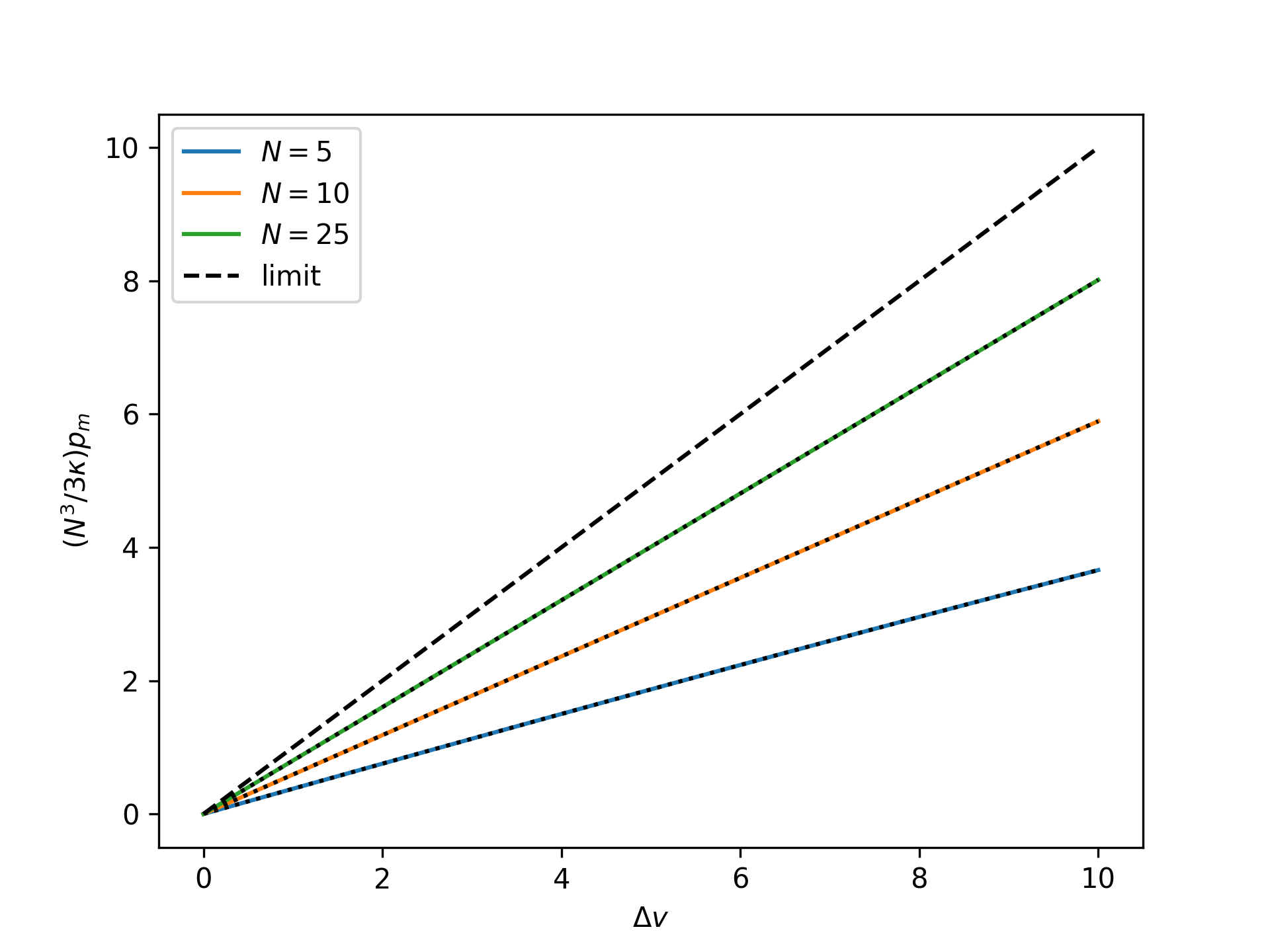
Plot the rescaled nondimensional end force as a function of the nondimensional end separation for the mechnically-treated system for an increasing number of broken bonds \(N\) and compare to the thermodynamic limit:
>>> import numpy as np >>> import matplotlib.pyplot as plt >>> from statmechcrack import CrackMechanical >>> v = np.linspace(1, 11, 33) >>> _ = plt.figure() >>> for N in [5, 10, 25]: ... model = CrackMechanical(N=N) ... p_m = model.p_mechanical(v) ... r_p_m = model.N**3/3/model.kappa*p_m ... _ = plt.plot(v - 1, r_p_m, label='$N=$'+str(N)) ... v_m = model.v_mechanical(p_m) ... _ = plt.plot(v_m - 1, r_p_m, 'k:') >>> _ = plt.plot(v - 1, v - 1, 'k--', label='limit') >>> _ = plt.xlabel(r'$\Delta v$') >>> _ = plt.ylabel(r'$(N^3/3\kappa)p_m$') >>> _ = plt.legend() >>> plt.show()
- v_0_mechanical(p, lambda_)[source]
The nondimensional end separation as a function of the nondimensional end force for the mechnically-treated reference system, calculated by minimizing the total potential energy.
- Parameters:
p (array_like) – The nondimensional end force.
lambda (array_like) – The intact bond stretches.
- Returns:
The nondimensional end separation.
- Return type:
numpy.ndarray
- v_b_mechanical(p, lambda_)[source]
The nondimensional end separation as a function of the nondimensional end force for the mechnically-treated isolated bending system, calculated by minimizing the total potential energy.
- Parameters:
p (array_like) – The nondimensional end force.
lambda (array_like) – The intact bond stretches.
- Returns:
The nondimensional end separation.
- Return type:
numpy.ndarray
- v_mechanical(p)[source]
The nondimensional end separation as a function of the nondimensional end force for the mechnically-treated system, calculated by minimizing the total potential energy.
- Parameters:
p (array_like) – The nondimensional end force.
- Returns:
The nondimensional end separation.
- Return type:
numpy.ndarray
Example
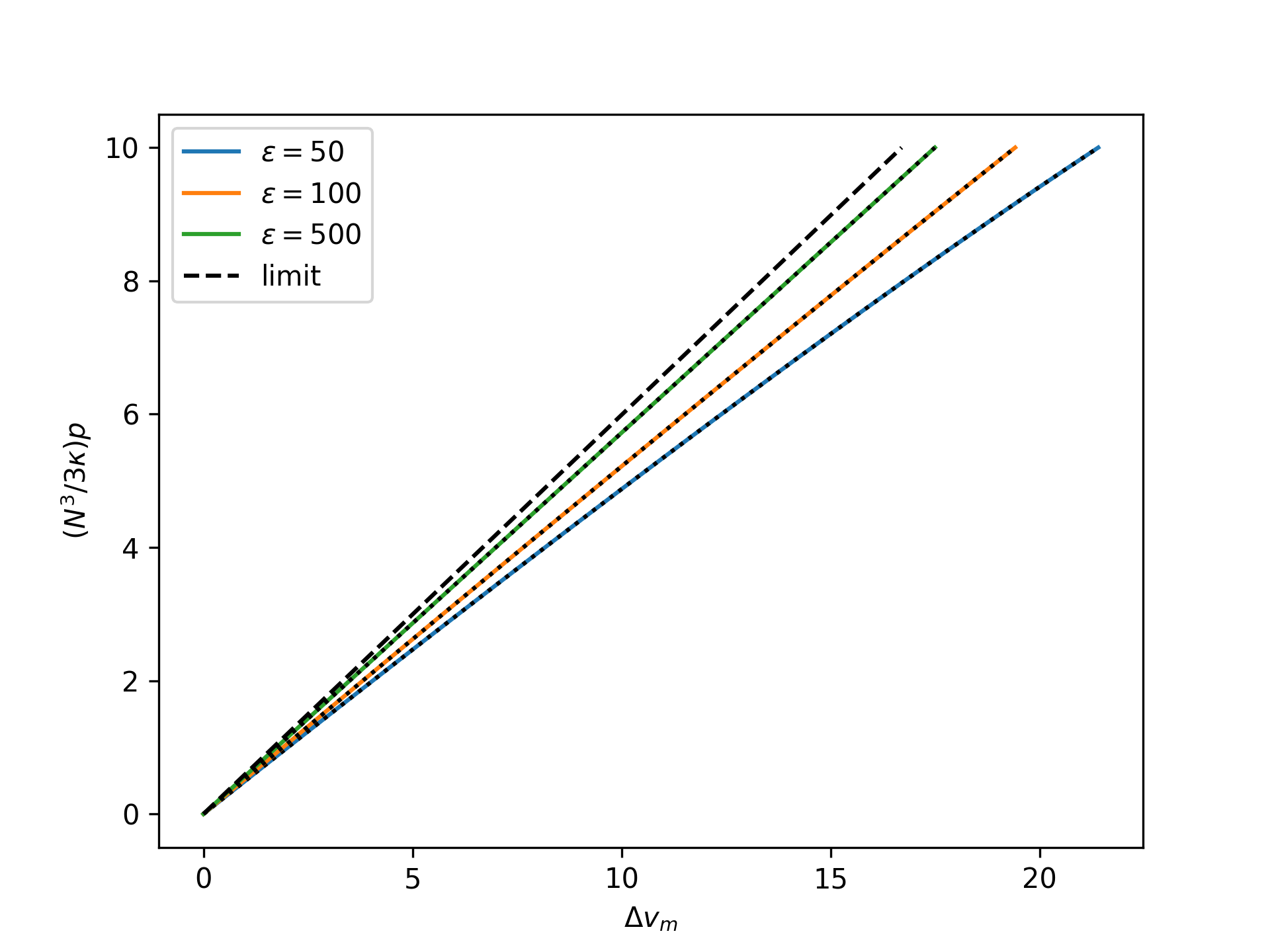
Plot the nondimensional end separation as a function of the rescaled nondimensional end force for the mechnically-treated system for an increasing nondimensional bond energy \(\varepsilon\) and compare to the limit given by the mechanically-treated reference system:
>>> import numpy as np >>> import matplotlib.pyplot as plt >>> from statmechcrack import CrackMechanical >>> v = np.linspace(1, 11, 33) >>> _ = plt.figure() >>> for varepsilon in [50, 100, 500]: ... model = CrackMechanical(varepsilon=varepsilon) ... r_p = np.linspace(0, 10, 33) ... p = 3*model.kappa/model.N**3*r_p ... v_m = model.v_mechanical(p) ... _ = plt.plot(v_m - 1, r_p, ... label=r'$\varepsilon=$'+str(varepsilon)) ... p_m = model.p_mechanical(v_m) ... r_p_m = model.N**3/3/model.kappa*p_m ... _ = plt.plot(v_m - 1, r_p_m, 'k:') >>> _ = plt.plot(model.v_0_mechanical(p, [1, 1]) - 1, ... r_p, 'k--', label='limit') >>> _ = plt.xlabel(r'$\Delta v_m$') >>> _ = plt.ylabel(r'$(N^3/3\kappa)p$') >>> _ = plt.legend() >>> plt.show()
References